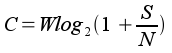Pour un signal numérique, on appelle débit binaire D la quantité d'informations émise par unité de temps par une source. L'unité de débit binaire est le bit par seconde ou bps.

Le débit binaire dépend des caractéristiques physiques du support de transmission et des techniques de transmission utilisées. Naturellement il ne possède de signification que dans le contexte de l'existence d'un signal. Par définition, le débit représente le nombre d'éléments binaires transmis par seconde, il est donc l'inverse de la durée d'un élement binaire ou intervalle significatif :

Plus concrètement, on pourra évaluer un débit si l'on connaît la quantité de bits à émettre et la durée de l'émission à partir d'une source. La formule pratique s'écrit :

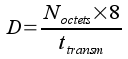
où N_octets représente le nombre d'octets à émettre et t_transm, le temps nécessaire pour émettre ces octets.

Exemple 1.4. calcul du temps d'émission

Calculons le temps d'émission d'un message de 512 octets en sortie d'une carte réseau fonctionnant à 100 Mbps.

La formule que nous venons de donner ci-dessus motnre que le temps d'émission est tout simplement égal au nombre de bits émis divisé par le débit, soit :

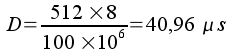
Dans le cas d'un signal analogique, on ne peut plus définir le débit d'information directement. Il faut pouvoir associer des tranches de temps du signal continu aux éléments binaires.

Un canal de transmission parfait n'existe pas dans la pratique et l'on est amené à considérer que le signal réellement transmis est la somme du signal à transmettre et d'un bruit additif. Le bruit d'un dispositif électronique est caractérisé par le rapport signal/bruit tel que :

dans laquelle S représente la puissance du signal et N celle du bruit. Pour un support (on dira aussi canal de transmission) donné, on définit la capacité d'un canal comme le débit binaire théorique maximum que ce canal peut supporter. La capacité C est évaluée à l'aide de la formule de Shannon :

	Important
	Équation 1.4. Formule de Shannon avec W, la largeur de la bande passante, S la puissance du signal et N la puissance du bruit inhérent à la ligne.

Exemple 1.5. Calcul de Capacité théorique

Calculons la capacité théorique du réseau MAP pour lequel la largeur de la bande passante vaut 12 MHz et le rapport signal/bruit vaut 26 dB

D'après la première formule ci_dessus, on a :

Nous trouvons donc notre rapport S/N = 398,11

En appliquant la formule de Shannon, il vient : C = 12.10⁶log₂(398,11), soit C = 103,5 Mbps.

En conclusion, nous dirons que le débit binaire sur un canal bruité est limité et que cette limite dépend de la bande passante du canal de transmission et de son rapport signal/bruit.

	quelques rappels sur les logarithmes
	Remarque épistémiologique : Les deux fonctions logarithmes les plus utilisées sont celles à base e = 2,71828... et à base 10. On les appelait respectivement autrefois le grand log (Log) et le petit log (log). aujourd'hui, logarithme népérien (ln) et logarithme à base 10 (log). Quelques propriétés : 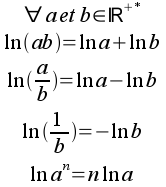Changement de base soit par exemple :