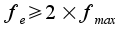Nous avons vu que pour réaliser un signal numérique à partir d'un signal analogique, il fallait l'échantillonner avec une fréquence d'échantillonnage :
puis il faut se fixer un foimprmat binaire de n bits pour exprimer chaque échantillon (quantification à 2n valeurs). Un problème survient si l'on désire ensuite reconstituer le signal analogique à partir du signal numérique. On montre que dans ce cas, il existe une contrainte sur la fréquence d'échantillonnage. Celle-ci doit être au moins égale au double de la fréquence maximale fmax du signal analogique.
![[Important]](images/important.png)
Exemple 1.2. Theorème de Shannon
Si l'on veut numériser le signal analogique du réseau téléphonique qui possède une bande passante s'étendant de 300 à 3400 Hz, quelle doit être la fréquence d'échantillonnage minimum ?
La formule du théorème de Shannon nous montre immédiatement que la fréquence d'échantillonnage doit être supérieure au double de la fréquence maximum, soit 6 800 Hz. La fréquence standard qui a été choisie dans le réseau numérique est de 8 KHz, ce qui satisfait les conditions ci-dessus.