Table des matières
L'encodage de l'information consiste à utiliser des codes pour représenter l'information afin de résoudre 3 types de problèmes :
Assurer l'intégrité de l'information (détection et correction d'erreurs
minimiser la taille de l'information (compression)
garantir la sécurité de l'information (encryptage/chiffrement)
Ces codes peuvent être combinés entre eux si nécessaire. Les codes assurant l'intégrité sont des codes de base utilisés systématiquement, alors que les deux autres types de code sont plus spécifiques et utilisés à la demande.
Les informations sont stockées sous forme binaire dans un ordinateur. Il arrive que ces données se corrompent un peu sou sl'effet d'un quelconque dysfonctionnement. Pour de petits problèmes, portant sur quelques bits isolés, l'intégrité des données est assurée par l'utilisation de codes détecteurs et correcteurs d'erreurs.
La compression a pour but de diminuer la taille nécessaire à la représentation d'une information, afin de réduire l'espace utilisé pour son stockage ou pour abréger le temps de transmission de l'information.
L'encryptage permet de garantir la sécurité des informations en empêchant tout accès non autorisé. La cryptographie consiste à coder des messages confidentiels avant de les transmettre grâce à la technique du chiffrement.
Toutes ces techniques d'encodage reposent sur l'utilisation d'algorithmes plus ou moins complexes dont nous allons vous décrire les plus représentatifs dans ce chapitre.
Une information peut subir des modifications involontaires lors de sa transmission ou lors de son stockage en mémoire. Il faut donc utiliser des codes permettant de détecter ou même de corriger les erreurs dues à ces modifications. Ces codes portent sur un nombre de bits supérieur à celui strictement nécessaire pour coder l'information. Aux m bits de données, on ajoute k bits de contrôle. Ce sont donc n = m + k bits qui vont être transmis ou stockés en mémoire. On parle de codes redondants.
Certains codes ne permettent que la détection des erreurs (codes autovérificateurs), d'autres permettent la détection et la correction d'une ou plusieurs erreurs (code autocorrecteurs).
Le contrôle de parité est le code autovérificateur le plus simple. Il se compose de m + 1 bits : les m bits d'information auxquels on ajoute un (m+1)-ème bit, dit de parité. Sa valeur est telle que le nombre total de bits à 1, calculé sur les m+1 bits, est pair (dans le cas d'une parité paire) ou impair (parité impaire.)
Exemple 3.1. Contrôle de parité
Transmission d'une suite de caractères codés en ASCII (7 bits) + 1 bit de parité
Tableau 3.1. Contrôle de parité impaire
| Lettre | bit de parité impaire | bit 1 | bit 2 | bit 3 | bit 4 | bit 5 | bit 6 | bit 7 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | → | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | ||||
| B | → | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | ||||
| C | → | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | ||||
| D | → | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | ||||
| E | → | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
Le bit de parité force le nombre total de bits à 1 à être impair, dans le cas d'une parité impaire.
Si un bit est changé par erreur pendant le transfert, la parité n'est plus vérifiée. L'erreur est détectée : il faut alors retransmettre l'information. S'il y a une double erreur dans le même caractère, la parité est vérifiée et la détection est alors impossible. D'une façon générale, le contrôle de parité ne permet de détecter qu'un nombre impair d'erreurs. Dans le cas d'un nombre pair d'erreurs, les effets s'annulent.
Les contrôles de parité de ce type ne peuvent être utilisés que pour des transmissions où le taux d'erreur est très faible (comme par exemple à l'intérieur d'un ordinateur ou entre un ordinateur et ses périphériques).
C'est le code obtenu en effectuant un double contrôle de parité.
Exemple 3.2. Double parité
Prenons l'exemple d'un nombre codé en ASCII (7 bits).
Pour le codage :
Chaque caractère est codé sur une ligne du tableau
Un code de parité impaire est effectué sur chaque ligne (contrôle transversal)
Un code de parité impaire est effectué sur chaque colonne (contrôle longitudinal)
Pour le décodage :
Le contrôle transversal permet de détecter une erreur sur la première ligne (le premier caractère)
Le contrôle longitudinal permet de détecter une erreur sur la quatrième colonne (bit numéro 4)
Le bit numéro 4 du premier caractère est faux, on peut le corriger
Tableau 3.2. Contrôle de parité impaire
| Caractère | Numéro de bit | Bit de parité | Contrôle transversal | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| 1. car. = 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | ← faux |
| 2. car. = 9 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | OK |
| 3. car. = 6 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | OK |
| 4. car. = 8 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | OK |
| bit de parité | 1 | 1 | 1 | 1 | 0 | 0 | 1 | ||
| contrôle longitudinal | OK | OK | OK | ↑ faux | OK | OK | OK | ||
La double parité permet donc de corriger une erreur ou même, dans certain cas, un nombre impair d'erreurs (comme, par exemple, trois bits en erreur sur une même colonne). Cependant, dans la plupart des cas, seule la détection d'un nombre impair d'erreurs est possible (comme, par exemple, trois bits répartis sur des lignes et des colonnes différentes).
le principe de la double parité est souvent utilisé dans le stockage sur bande magnétique. Pour une bande à n pistes :
Chaque caractère est stocké transversalement sur (n-1) pistes
1 bit de parité transversale est stocké sur la nième piste
Tous les m caractères (1 bloc), on effectue un contrôle de parité longitudinale un peu plus poussé (checksum)
Le code de Hamming est un code autocorrecteur, basé sur les tests de parité. La version la plus simple permet de corriger un bit en erreur.
Aux m bits d'information, on ajoute k bits de contrôle de parité. On a donc m + k = n bits. Puisque les k bits de contrôle doivent indiquer les n + 1 possibilités d'erreurs (dont l'absence d'erreur, ce qui explique le +1), il faut que 2k≥n + 1. Les 2k possibilités de codage sur les k bits servent à coder la position de l'erreur. Dès que cette position est calculée, on peut corriger le bit en erreur.
Le tableau suivant permet de déterminer k quand on connaît n :
Tableau 3.3. Contrôle de parité impaire
| m | 0 | 0 | 1 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... | 120 | ... | |
| k | 1 | 2 | 2 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | ... | 8 | ... | |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ... | 128 | ... |
On a intérêt à choisir les codes à redondance minimale qui donnent un maximum de positions d'information, c'est-à-dire à prendre n = 2k - 1 au lieu de n ≺ 2k - 1
Si l'on numérote les bits de droite à gauche à partir de 1, les bits de contrôle (ou de parité) sont placés sur les puissances de 2 (bits n° 1, 2, 4, 8, 16...) .Chaque bit de contrôle effectue un contrôle de parité (paire ou impaire) sur un certain nombre de bits de données. On détermine ainsi les n bits à transmettre ou à stocker. Il faut noter que le premier bit à droite porte le numéro 1 et non pas 0.
Exemple 3.3. Code de hamming 1
Si le nombre de bit d'information est 4 (m=4), on peut construire un code de Hamming sur 7 bits (n=7) en ajoutant 3 bits de contrôle (k=3).
Les 3 bits de contrôle k3, k2 et k1 sont placés sur les puissances de 2 : k1 en position 1, k2 en position 2 et k3 en position 4
Nous allons voir maintenant, pour chaque bit du message, quels sont les bits de contrôle qui permettent de vérifier sa parité :
Tableau 3.5. Code de Hamming 1
| 7 | (0111) | = | 4 + 2 + 1 | → | 7 | est contrôlé par k3, k2, k1 |
| 6 | (0110) | = | 4 + 2 | → | 6 | est contrôlé par k3, k2 |
| 5 | (0101) | = | 4 + 1 | → | 5 | est contrôlé par k3, k1 |
| 4 | (0100) | est le bit contrôle k3 | ||||
| 3 | (0011) | = | 2 + 1 | → | 3 | est contrôlé par k2, k1 |
| 2 | (0010) | est le bit contrôle k2 | ||||
| 1 | (0001) | est le bit contrôle k1 | ||||
Ou inversement, qui contrôle qui ?
k1 contrôle les bits 1, 3, 5, 7
k2 contrôle les bits 2, 3, 6, 7
k3 contrôle les bits 4, 5, 6, 7
Avec une parité paire, par exemple, k1 doit être tel que le nombre de bits à 1, compté sur les bits 1, 3, 5 et 7 soit pair.
Quand on reçoit ou que l'on relit l'information, on effectue à nouveau le contrôle de la parité. Pour chacun des bits de contrôle, on compare la valeur reçue, ou relue, à celle recalculée :
Si elles sont identiques, on assigne la valeur 0 à la variable binaire Ai associée au bit de contrôle ki
Sinon, on lui assigne la valeur 1
Exemple 3.4. Code de Hamming 2
Reprenons l'exemple précédent :
Supposons que la valeur associée à k1 soit A1=1;
Supposons que la valeur associée à k2 qoit A2=1;
Supposons que la valeur associée à k3 qoit A3=0;
On sait alors qu'une erreur se trouve dans la transmission suivante : A3A2A1=011
Une erreur détectée en faisant intervenir k1 ne peut venir que des bits dont l'adresse binaire se termine par 1, c'est-à-dire 1,3,5 ou 7. De même, le test k2 porte sur les bits 2, 3, 6, 7. Enfin, le contrôle k3 porte sur les bits 4, 5, 6, 7. Une erreur détectée par k1 et k2 mais pas par k3 ne peut donc provenir que du bit 3 = 0112.
![[Note]](images/note.png) | Note |
|---|---|
Vous comprenez maintenant que la valeur A3A2A1=000 indique une absence d'erreur. la valeur A3A2A1=001 indique une erreur sur le bit numéro 1. la valeur A3A2A1=110 indique une erreur sur le bit numéro 6. |
Exemple 3.5. Code de Hamming : réception d'un message
Supposons que l'on reçoive le message suivant : 1011100.
Sachant que le code utilise une parité paire, retrouver le message initial.
Le nombre n de bits transmis est égal à 7. On a donc k=3 bits de contrôle, et m=4 bits d'information
k1=0 (bit 1,3,5,7) est donc faux →A1=1
k2=0 (bit 2,3,6,7)est donc bon →A2=0
k3=1 (bit 4,5,6,7) est donc faux →A3=1
L'adresse binaire de l'erreur est : A3A2A1=101=5. Le bit 5, qui vaut 1, est faux.
Le message initial corrigé est : 1001100 et, si l'on ôte les bits de parité, on obtient les données initiales : 1001.
On peut simplifier le calcul des bits de contrôle dans la méthode de hamming pour la détection et la correction d'une seule erreur.
Exemple 3.6. Calcul simplifié du code de Hamming - Transmission d'un message
Coder 1010 1011 001 avec une parité paire : m=11, donc k=4.
Le message à transmettre contient n=15 bits.
Tableau 3.7. Code de Hamming 1
| numéro | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| type | m11 | m10 | m9 | m8 | m7 | m6 | m5 | k4 | m4 | m3 | m2 | k3 | m1 | k2 | k1 |
| valeur | 1 | 0 | 1 | 0 | 1 | 0 | 1 | ? | 1 | 0 | 0 | ? | 1 | ? | ? |
Dans le message à transmettre, on a des bits à 1 dans les positions suivantes : 15, 13, 11, 9, 7, 3.
On transforme ces positions en leur valeur binaire et on les additionne modulo 2 : On met 1 lorsque l'on a un nombre impair de 1 et 0 pour un nombre pair de 1.
Tableau 3.8. Code de Hamming 1
| 15 | = | 1 | 1 | 1 | 1 | |
| 13 | = | 1 | 1 | 0 | 1 | |
| 11 | = | 1 | 0 | 1 | 1 | |
| 9 | = | 1 | 0 | 0 | 1 | |
| 3 | = | 0 | 0 | 1 | 1 | |
| ---------- | ||||||
| 0 | 1 | 0 | 0 | → bits de parité | ||
| k4 | k3 | k2 | k1 | |||
Le message codé est donc 1010 1010 1001 100.
Dans le cas d'une parité paire, on fait simplement une addition modulo 2. Pour une parité impaire, il faut faire une addition modulo 2 inversée :
nombre impair de 1 → 0
nombre pair de 1 → 1
Exemple 3.7. Calcul simplifié du code de Hamming - Réception d'un message
On a reçu le message suivant : 1010 0010 1001 100. La parité utilisée est impaire. On a des bits à 1 dans les positions :
Tableau 3.9. Code de Hamming 1
| 15 | = | 1 | 1 | 1 | 1 | |
| 13 | = | 1 | 1 | 0 | 1 | |
| 9 | = | 1 | 0 | 0 | 1 | |
| 7 | = | 0 | 1 | 1 | 1 | |
| 4 | = | 0 | 1 | 0 | 0 | |
| 3 | = | 0 | 0 | 1 | 1 | |
| ---------- | Addition modulo 2 inversée | |||||
| 0 | 1 | 0 | 0 | |||
| A4 | A3 | A2 | A1 | → erreur à la position 4 | ||
Après la correction du bit en position 4, on a le message suivant : 1010 0010 1000 100
Ce message corrigé a des bits à 1 dans les positions :
Tableau 3.10. Code de Hamming 1
| 15 | = | 1 | 1 | 1 | 1 | |
| 13 | = | 1 | 1 | 0 | 1 | |
| 9 | = | 1 | 0 | 0 | 1 | |
| 7 | = | 0 | 1 | 1 | 1 | |
| 3 | = | 0 | 0 | 1 | 1 | |
| ---------- | Addition modulo 2 inversée | |||||
| 0 | 0 | 0 | 0 | → aucune erreur détectée | ||
Les données originales, après avoir éliminé les bits redondants sont : 1010 0011 001
La méthode de Hamming peut seulement corriger une erreur. Mais on peut l'utiliser dans le cas d'erreurs multiples sur une séquence de bits arrangeant le message de façon matricielle.
Exemple 3.8. Arrangement matriciel du code de Hamming
Tableau 3.11. Code de Hamming 1
| ASCII | Code de Hamming (pour chaque lettre) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| H → 1001000 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| a → 1100001 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| m → 1101101 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| m → 1101101 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| i → 1101001 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| n → 1101110 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| g → 1100111 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
On effectue le codage ligne par ligne et on transmet les bits colonne par colonne. S'il se produit des erreurs groupées (sur une séquence de bits assez courte, ≤7 pour cet exemple), alors en effectuant la transmission par colonne, on aura un seul bit erroné par ligne. On peut le corriger grâce aux bits de contrôle ajoutés selon la méthode de Hamming.
Dans les transmissions à distance, les erreurs sont beaucoup plus fréquentes qu'à l'intérieur des ordinateurs. Les erreurs consécutives à un bruit, par exemple, portent souvent sur tout un bloc de bits.
Exemple 3.9. Erreur groupée sur une ligne téléphonique
Sur une ligne téléphonique, un bruit, un clic, d'une durée de ≈ 1/100e de seconde, passe presque inaperçu pendant une conversation, mais ce bruit peut détruire une bloc de 96 bits dans une transmission de données à 9 600 bps !
On va donc utiliser des codes qui permettent la détection d'erreurs groupées, la correction étant trop coûteuse (en bits de contrôle, calculs de parité...)
le CRC (ou méthode des codes polynômiaux) est la méthode la plus utilisée pour détecter des erreurs groupées. Avant la transmission, on ajoute des bits de contrôle. Si des erreurs sont détectées à la réception, il faut retransmettre le message.
Une information de n bits peut être considérée comme la liste des coefficients binaires d'un polynôme de n termes, donc de degré n-1.
Pour calculer les bits de contrôle, on va effectuer un certain nombre d'opérations avec ces polynômes à coefficients binaires.Toutes ces opérations seront effectuées modulo 2. C'est ainsi que, dans les additions et dans les soustractions, on ne tiendra pas compte de la retenue : Toute addition et tout soustraction sont donc identiques à une opération XOR.
La source et la destination choisissent un même polynôme G(x) dit générateur car il est utilisé pour générer les bits de contrôle (Checksum).
L'algorithme pour calculer le message à envoyer est le suivant. Soit M(x) le polynôme correspondant au message original, et soit r le degré du polynôme générateur G(x) choisi :
Multiplier M(x) par xr, ce qui revient à ajouter r zéros à la fin du message original
effectuer la division suivante modulo 2 :

Le quotient Q(x) est ignoré. Le reste R(x) (Checksum) contient r bits (degré du reste r-1). On effectue alors la soustraction modulo 2 :

Le polynôme T(x) est le polynôme cyclique : c'est le message prêt à être envoyé. Le polynôme cyclique est un multiple du plynôme générateur T(x) = Q(x).G(x)
A la réception, on effectue la division suivante :

Si le reste = 0, il n'y a pas d'erreur
si le reste ≠ 0, il y a erreur, donc on doit retransmettre
En choisissant judicieusement G(x), on peut détecter toute erreur sur 1 bit, 2 bits consécutifs, une séquence de n bits et au-delà de n bits avec une très grande probabilité.
Exemple 3.13. CRC - Transmission d'un message
On doit transmettre le message : 101101 (6 bits) → M(x) = x5+x3+x2+1
Le polynôme générateur choisi est : 1011 (4 bits) → G(x) = x3+x+1 de degré r=3.
Effectuons la multiplication : M(x).xr = 101101000.
On a ajouté r = 3 zéros à M(x)
Division modulo 2 de M(x) / G(x)
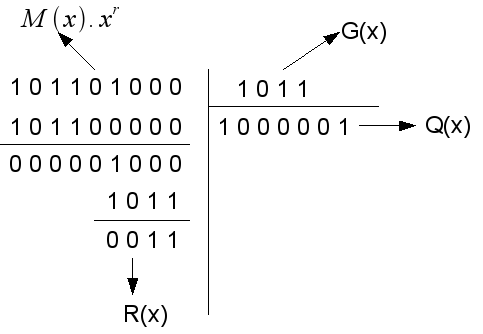
Transmission - Division, modulo 2
Le quotient Q(x) est ignoré
Pour soustraire modulo 2, le reste R(x) de M(x).xr, il suffit d'ajouter les r bits de R(x) à la fin de M(x) → le message à transmettre : T(x) = 101101011
Les polynômes générateurs G(x) les plus utilisés sont les suivants :
CRC-12 = x12+x11+x3+x2+x+1
CRC-16 = x16+x15+x2+1
CRC-CCITT = x16+x12+x5+1
le CRC-CCITT, recommandé pour les caractères de 8 bits, détecte toutes les erreurs groupées en bloc ≥ 17 bits.
Exemple 3.14. CRC - Réception d'un message
On a reçu le message suivant : 11010101. G(x) = 1011 → degré r=3.
On effectue la division T(x) / G(x) :

Réception - Divisio, modulo 2
R(x) ≠ 0. Il y a donc des erreurs de transmission. Il faut retransmettre le message.