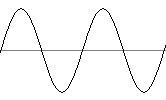
Nous avons vu, jusque là, des courbes parfaites. En comparaison avec le monde du son, imaginons la note LA.
L'amplitude déteriminera la puissance du son (grande amplitude = son fort, petite amplitude = son faible)
La période déterminera la "hauteur" du son. Plus la période est longue, plus le son sera grave. Naturellement, plus elle est courte, plus le son sera aigü
Sur les différentes représentations des courbes suivantes, les fréquences et les amplitudes sont identiques.
Cette courbe n'est plus parfaite.
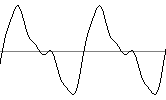
une harmonique s'ajoute sur la courbe parfaite Son de cette courbe
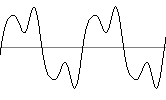
une harmonique s'ajoute sur la courbe parfaite Son de cette courbe
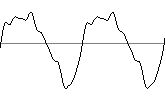
une harmonique s'ajoute sur la courbe parfaite Son de cette courbe
Nous avons vu précédemment que toute courbe périodique peut être décomposer en un nombre fini (ou infini) de sinusoïdes. Il s'agit de la décompositions en séries de Fourier.
Parmi l'exemple des sons que nous vous proposons, vous pouvez distinguer un son pur qui se limite à une seule sinusoïde.
La première sinusoïde a pour fréquence la fondamentale. Les autres sinusoïdes ont des fréquences qui en sont des multiples.